この記事は古川研究室 Advent Calendar13日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。
本記事では、PCAこと主成分分析について理解した”い”をコンセプトに記事を書きました。
はじめに
まずPCAについてざっくりと書きます。
主成分分析とは、多次元の次元を下げる教習なし学習のことです。多次元データを人間が見やすいように2次元や3次元に落とし込むといったことを行います。低次元空間へ落とし込むとき、データの情報をできるだけ損なわないように、つまりデータの情報を最も含むように(分散値が大きくなるよう)にして落とし込みます。
何が嬉しいのか
では次元削減することで何が嬉しいのでしょうか?
例えば、ワインの成分には水、エタノール、有機酸、糖、グリセリン、アミノ酸、核酸、タンニン、炭酸ガスがあり9次元データになります。これらのデータにワインの評価を含めて10次元データを考えてみましょう。関係性を図やグラフなどで可視化することで"どういう成分比のときに評価値が高いのか"といったことを把握したいですが、我々人間には4次元以上の次元はわかりにくいです。そこで、PCAで我々人間が見やすい2次元、3次元に次元を落とそうとしてPCAを使うわけです。
主成分分析
主成分分析では、データの情報を主成分軸という軸に情報を落とし込みます。3次元に落とし込むなら3本の主成分軸、2次元に落とし込むなら2本の主成分軸です。
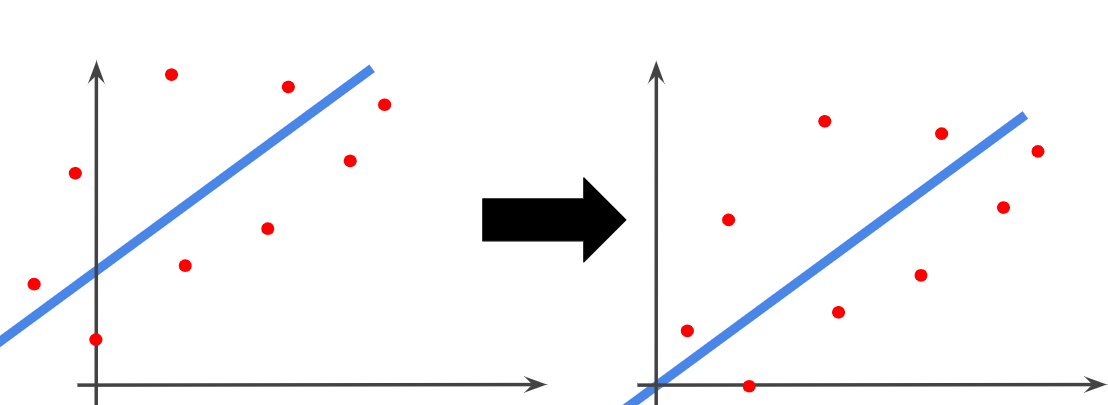
注意してほしいことは、”空間を平面に"、"平面を直線に"落とし込んでいるのではなく、高次元から低次元への射影を行っているのです。
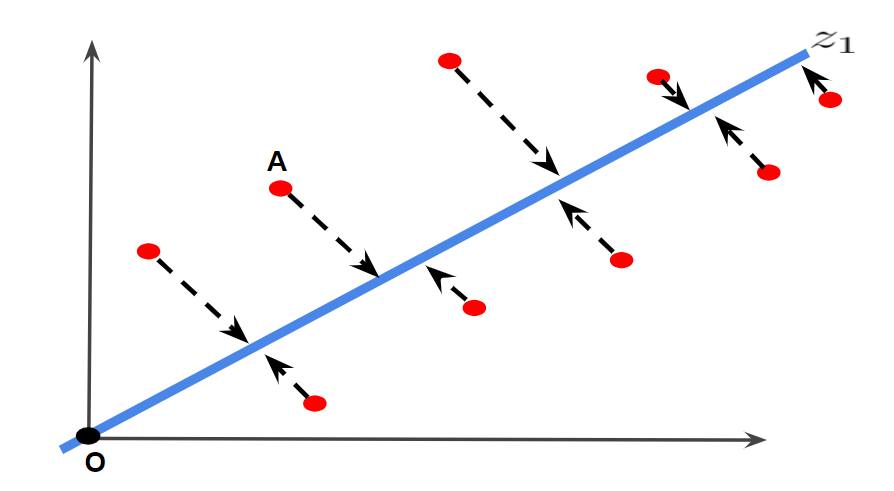
下図はイメージ図です。赤点のデータ点を1本の主成分軸に落とし込んでいます。
前処理
PCAの前処理として中心化というのがあります。中心化ではデータの値から、それらの平均値を引くことで平均0にすることです。これにより、データは原点を中心に分布します。
$$x_{ip}=x_{ip}-\bar{x_p}$$
中心化する理由としては後述します。
どのようにしてやるのか
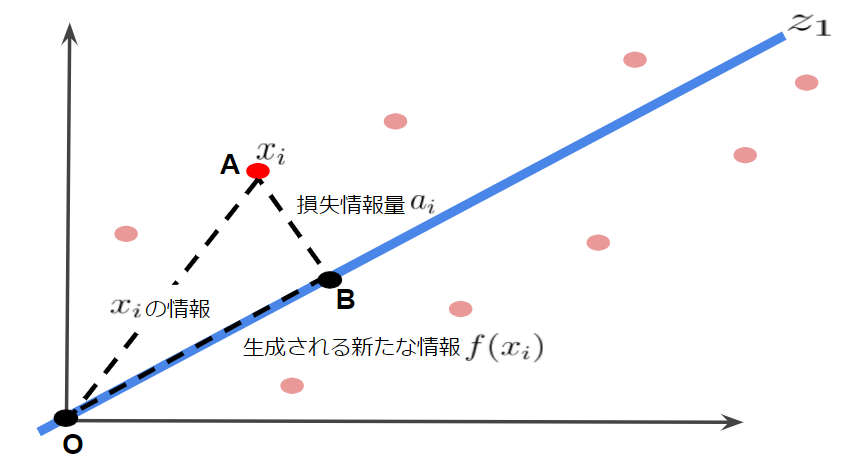
主成分分析では、情報をできるだけ損なわずにデータを射影します。裏を返せば得られる情報量が最大になればいいということです。したがって、次元削減して得られたデータの分散が最大になればいいということです。これを図を用いて考えてみます。ここで9つのデータの1つのデータAに着目します。データを第1主成分$z_1$で表す場合、$x_i$の情報損失量は主成分軸$z_1$に対して垂線を引いた$\vec{AB}$です。
ここで、ピタゴラスの定理から$\vec{OA}^2=\vec{AB}^2+\vec{OB}^2$の関係が成り立ちます。このとき、データAの情報量は$\vec{OA}$で、得られる新たな情報量が$\vec{OB}$になり主成分得点と言います。
したがって、9点のデータに対して以下の関係性が成り立ちます。
”元情報量の2乗和=新たな情報量の2乗和+損失情報量の2乗和”
この関係性からわかりますが、損失情報量を最小にすると、新たな情報量が最大になるのがわかります。
この考えは多変数の場合も同じです。したがって、
主成分分析とは変数$x_1,x_2,x_3,\dots,x_p$をできるだけ元々の情報量を損なわないように、N個の主成分$z_1,z_2,z_3,⋯,z_N$に変換する手法のことです。つまり、P次元からN次元へ縮小
$$z_{n}=w_{11}x_1+w_{12}x_2 + w_{13}x_2 + \cdots + w_{1m}x_m=\sum_{i=1}^{N}x_iw_{ip}~(p=0,1,2,\dots,N)$$
$z_1$が第1主成分、$z_2$が第2主成分、$z_n$が第n主成分と言います。
主成分分析では、損失情報量を最小にすると、新たに得られる情報量が最大になります。この特性を利用して新たな情報量を最大化する最適化問題として扱うことができます。
$$\max_{w}~\frac{1}{N}\sum_{i=1}^Nf(x_i)^2=\frac{1}{N}\sum_{i=1}^N(x_iw_{ip})^2$$
$$subject~~to~~~~~~~w^Tw=1$$
このsubject toは制約条件です。$w^Tw$は主成分軸$z$に対して$w$に正規直交基底の役割を持たしています。
式を変形していきます。
$$\begin{equation*}\begin{split}\frac{1}{N}\sum_{i=1}^N(x_iw_{ip})^2&= \frac{1}{N}\sum_{i=1}^N(x_iw_{ip})^T(x_iw_{ip})\\&=\frac{1}{N}\sum_{i=1}^{N}w_{ip}^{T}x_{i}^Tx_{i}w_{ip}\\&=\frac{1}{N}w^T\sum_{i=1}^N(x_i^Tx_i)w\\&=w^TX^TXw\end{split}\end{equation*}$$
この式の$X^TX$は$N \times D$の行列であり、それぞれの要素は$x_i-\bar{x}$です。したがって、$X^TX$は分散・共分散行列になります。
ここで主成分分析の最適化問題を行列として表現します。
主成分分析の最適化問題
$$\max_{w}~\frac{1}{N}w^T \Omega w$$
$$subject~~to~~~~~~~w^Tw=1$$
$\Omega=X^TX$は学習データの分散・共分散行列
上記の式において制約条件がない場合を考えると、明らかに解$w$は$\infty$であることがわかります。
制約条件の付いた最適化問題を解く手法としてラグランジュの未定乗数法があります。本記事ではラグランジュの未定乗数法を用います。
ラグランジュの未定乗数法
ラグランジュの未定乗数法自体については別記事を参考にしてください。
まず、最適化問題からラグランジュ関数$L(\lambda,w)$の作成をします。
$$L(w,\lambda)=w^T \Omega w-\lambda(w^Tw-1)$$
変数$w$について偏微分すると
$$\frac{\partial L}{\partial w} = (\Omega+\Omega^T)w-2\lambda w=0$$
$\Omega$は分散・共分散行列であり対称行列なので$X=X^T$が成り立つ。したがって次の式が成り立つ。
$$2\Omega w-2\lambda w=0$$
$$\begin{equation}\Omega w = \lambda w\end{equation}$$
変数$\lambda$について偏微分すると
$$\frac{\partial L}{\partial \lambda} = -w^Tw-1=0$$
$$w^Tw=1$$
これら$\begin{equation}\Omega w = \lambda w\end{equation}$、$w^Tw=1$から主成分分析の最適化問題はラグランジュ未定乗数$\lambda$を固有値、ベクトル$\lambda$を固有ベクトルとした分散・共分散行列$G$の固有値問題ということがわかる。
-

-
固有値と固有ベクトルをわかりやすく書いてみた
この記事は古川研究室 Advent Calendar4日目の記事です。 本記事は古川研究室の学生が学 ...
続きを見る
したがって、分散・共分散行列$G$の固有値問題を解くことで最大となる固有値$\lambda*$を求め、それに対応する固有ベクトル$w*$を求めることで主成分軸が得られる。
分散・共分散行列$G$の固有値問題
$$\max_{\lambda}~\Omega w = \lambda w$$
$$subject~~to~~~~~~~\lambda\geqq0$$
以上のことを踏まえるとPCAのアルゴリズムは学習データ$x$が与えられたとき次のようになる。
PCAのアルゴリズム
①$x_i-\overline{x}$により中心化を行う
②分散・共分散行列$X^TX$を解く
③下記の固有値問題を解く$$\max_{\lambda}~\Omega w = \lambda w~~~~~~~~~subject~~to~~~~~~~\lambda\geqq0$$
④得られる固有値$\lambda$をそれぞれ$\lambda_1 \geqq \lambda_2 \geqq \lambda_2 \dots \geqq \lambda_d \geqq 0$とする。
⑤それぞれの固有値に対応する固有ベクトル$w_1,w_2,\dots,w_d$を主成分軸の正規直交基底とし、縮小したい次元(2次元なら2個)分を選択する。このとき、$w_1,w_2,\dots$を順に第1主成分、第2主成分,,,となる。
⑥選択した固有ベクトル$w_1,w_2\dots,w_D$の行列$W(w_1,w_2\dots)$の行列を作成し、学習データを低次元空間へ写像したときの主成分得点$F=(f_1(x_1),f_2(x_2),\dots,f_D(x_D))$を算出する。
$$F(X)=XW$$
ここまでが、PCAの理論になります。時間に余裕があれば特異点を使ってPCAを解く側面を書きたいと思います。
終わりに
ここまで読んでくださってありがとうございました.
編集リクエストもお待ちしてます()