[活性化関数]ステップ関数とシグモイド関数をわかりやすく

本記事では活性化関数の、ステップ関数とシグモイド関数を紹介したいと思います。

ニューラルネットワークやディープラーニングを理解しようと思ったら、活性化関数の理解は必須になります。

活性化関数にはパーセプトロンの知識があると容易に理解できます。パーセプトロンについては以下の記事を参照してください。

活性化関数とは

活性化関数とは、入力の信号を出力信号に変換する関数のことです。

入力(信号)の総和を、どのように活性化(発火とも言います)させるかを決定させます。

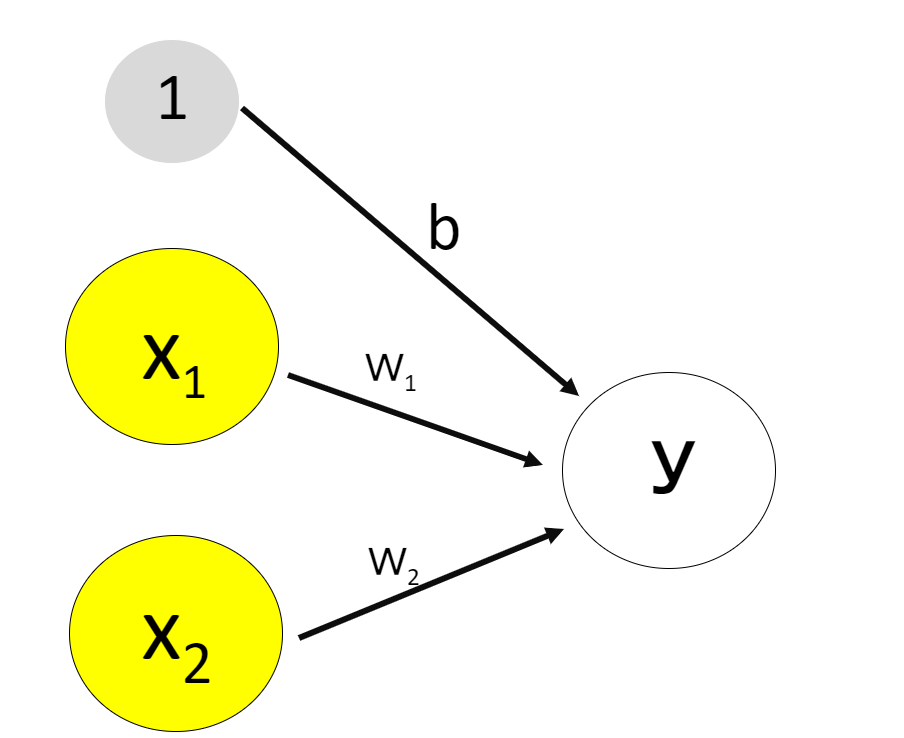
例えば、下の図のように3つのノードからの入力があるとしまし。
一番上の❶はバイアスと言われるものです。バイアスをコントロールすることで、出力（発火）のしやすさをコントロールします。

このときの入力の式を書くと

\[
y = \begin{cases}
1 & h(X) \ge 0 \ \text{のとき} \\
0 & h(X) < 0 \ \text{のとき}
\end{cases}
\]

$$h(X) = X_1W_1+X_2W_2+b$$

になります。この$h(X)$を活性化関数といいます。この場合の活性化関数は、入力の総和が0より大きいかどうかで1を出力(発火)します。

この活性化関数にはステップ関数とシグモイド関数というのがあります。それらの特徴を見ていきましょう。

ステップ関数

ステップ関数は階段関数とも呼ばれており、先ほどの例の活性化関数がステップ関数になります。式で表すと、

\[
y = \begin{cases}
1 & h(X) \ge 0 \ \text{のとき} \\
0 & h(X) < 0 \ \text{のとき}
\end{cases}
\]

です。

h(X)が0を超えるかどうかで1を出力します。0を超えない場合は0を出力します。

pythonコードで実装して見ていきましょう。

関数定義

import numpy as np
import matplotlib.pylab as plt 
def step_function(A): 
   return np.array(A > 0 , dtype=np.int)

まず、ステップ関数を定義します。これは、Aの値が0より大きいなら1を返し、それ以外は0を返すというものです。

データの用意

w = np.array([[2.1, 0.2, -1.2],[0.2, 0.3, 0.9]])
b = np.array([1, 0.1, 0.3])
x = np.array([1.1, 0.6])

重みパラメータとバイアスパラメータ、入力信号の値を用意しました。

これを、$h(X) = X_1W_1+X_2W_2+b$に代入して計算して、ステップ関数に入力します。

A = np.dot(x,w)+b    #出力結果:[ 3.43  0.5  -0.48]
y = step_function(A)
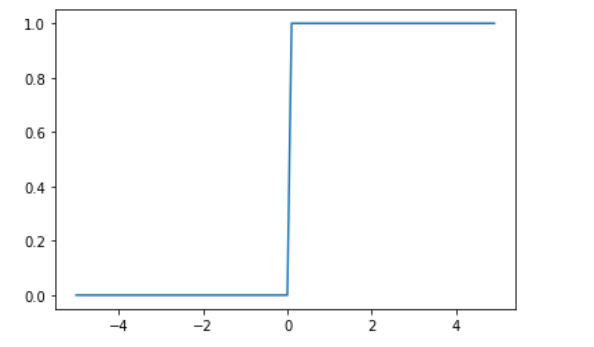
print(y)                         #出力結果:[1 1 0]  しっかりと0より大きい場合は1を出力して、小さい場合は0を出力できていますね。

ステップ関数は、グラフで表すと下図のようになります。

 0を境にして値が変わってます。

このように、階段的に変化するから階段関数とも言われています。

シグモイド関数

シグモイド関数は、以下の式で表されます。

$$y = \frac{1}{1 + e^{-x}}$$

これだけです。

実際に実装していきましょう。

ステップ関数で行ったことを省くため、データの用意などのプログラムを全て入れます。

import numpy as np
import matplotlib.pylab as plt
#関数定義
def sigmoid(A):
return 1 / (1 + np.exp(-x))
#データの用意
w = np.array([[2.1, 0.2, -1.2],[0.2, 0.3, 0.9]])
b = np.array([1, 0.1, 0.3])
x = np.array([1.1, 0.6])
#計算式に代入して、シグモイド関数に入力する
A = np.dot(x,w)+b
y = sigmoid(A)
print(y)
----------------------------
[0.75026011 0.64565631]

ステップ関数と違って、実数の値を出力しているのがわかりますね。
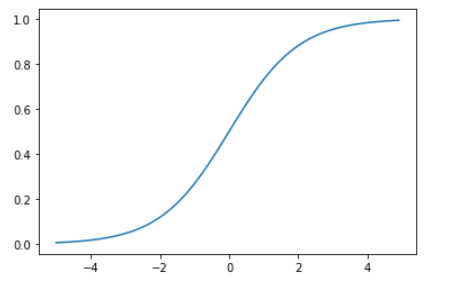
一般に、シグモイド関数は下図で表されます。ステップ関数と違い滑らかな曲線を描くのが特徴です。