最近、ロジスティック写像を使う機会がありました。
ロジスティック写像のことを調べていると、思っていた以上に難しいので自分なりに理解しようと記事にしてみました。
本記事では、そのロジスティック写像についての記事になります。
概要
ロジスティック写像は1次元の離散時系列であり、 時系列解析の研究のベンチマークデータとして用いられています。なぜなら、ロジスティック写像はカオスを生み出す非線形関数であり、その非線形関数の中では単純なものであり扱いやすいからです。この単純さと、他のカオスとも共通する現象がいくつも現れることからカオス理論の入り口としてもよく扱われます。
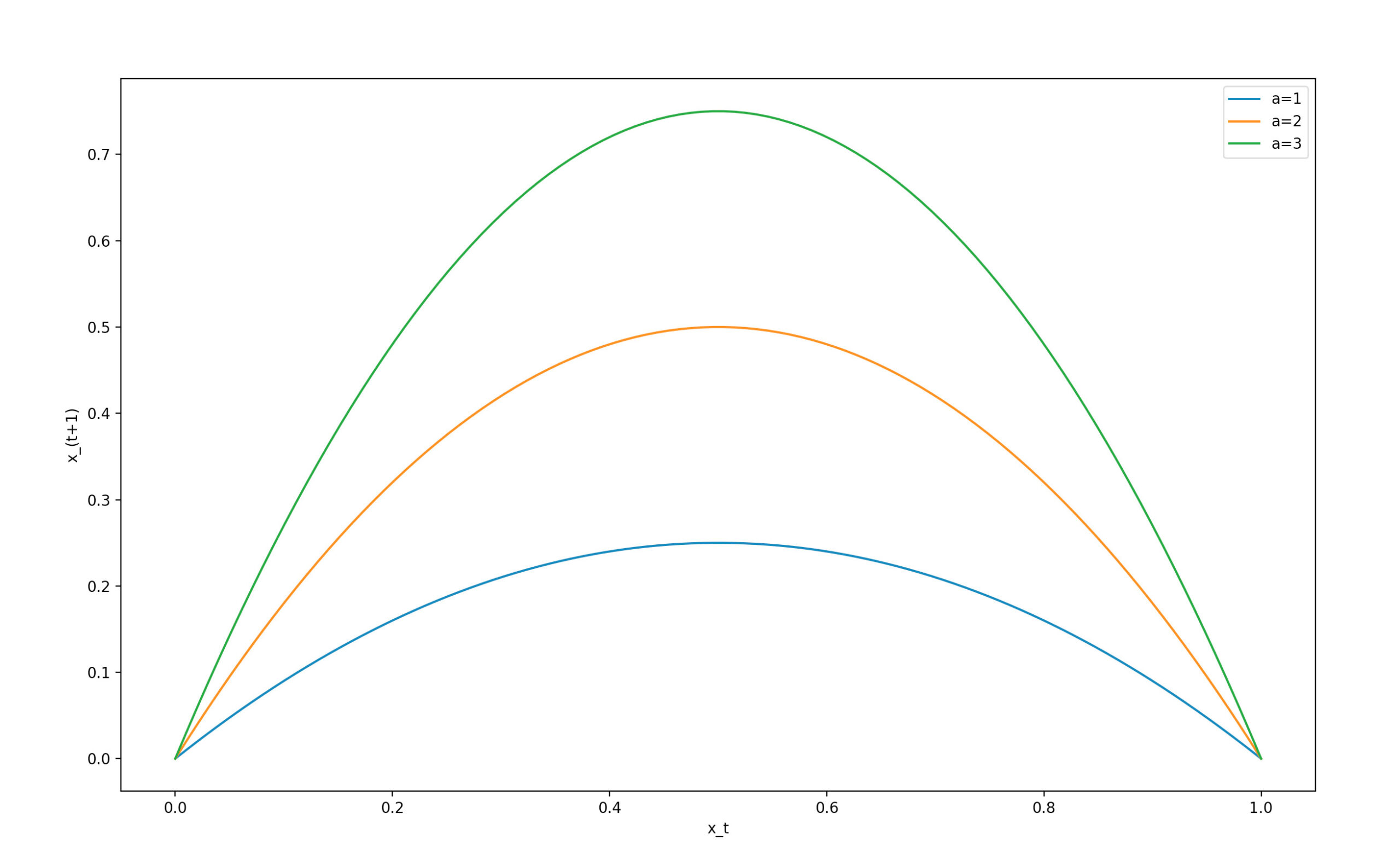
ロジスティック写像は下記の差分方程式で表され、図のように山形の曲線を描きます。また、$a$の値によって山の大きさが変わります。
$$x_{t+1}=ax_t(1-x_t)$$
蜘蛛の巣図法
ロジスティック写像がどういった振る舞いをするのかを表現するためには、蜘蛛の巣図法を用いる必要があります。
蜘蛛の巣図法とは、一次元離散力学系の振る舞いを図式的に表す手法のことを言います。
蜘蛛の巣図法では、下記の図のように補助線と言われる$y=x$の関数を使います。
離散力学系って?
力学系とは状態の変化の法則を記述した数学モデルのことで、離散力学は常差分方程式系 (漸化式)として表されます。力学系は下式(1次元離散力学系の式)のように出力が次の入力となります。
$$ x_{t+1}=f(x_t)$$
では蜘蛛の巣図法を詳しく見ていきます。
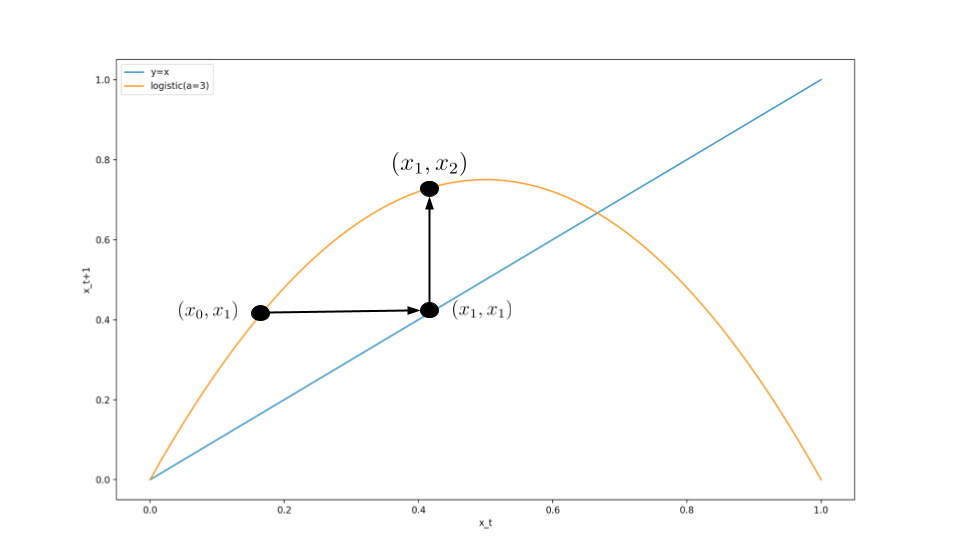
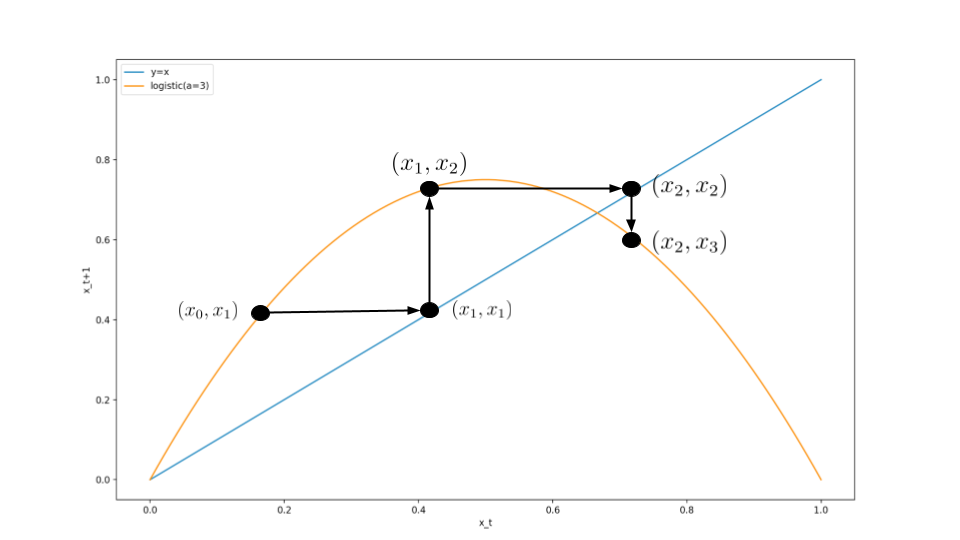
蜘蛛の巣図法では$y=x$の補助線を引きます。この補助線のおかげで、力学系の出力が次の入力になることを表すことができます。
下図で見てみます。
$y=x$のおかげで、力学系の出力が次の入力になることを表すことができています。
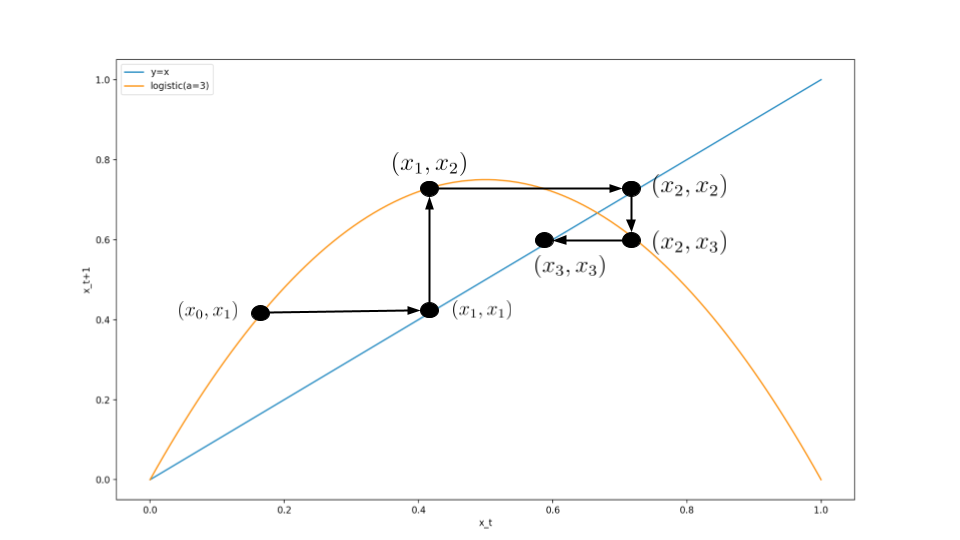
では、この蜘蛛の巣図法について100エポックほどの挙動を見てみましょう。
まるで、蜘蛛の巣のような図になっていきます。
この蜘蛛の巣図法によって、差分方程式の解の挙動が一目でわかる全体像がわかるのです。
パラメータ$a$の違いによる振る舞い
概要のところでロジスティック写像は$a$が異なることで山の大きさが変わると言いました。
$$x_{t+1}=ax_t(1-x_t)$$
この山の大きさによってロジスティック写像の振る舞いがどのように変わるのかを見ていきたいと思います。
$0\leqq a \leqq 1$のとき
$a=0.5$、初期値が$x_0=0.5$のときロジスティック写像は$y=x$との交点(不動点)である$0$へ収束します。
初期値が$0$から$1$の範囲でどんな値をとっても同じ現象になります。
最終的に収束していく点を固定点、不動点あるいは吸引的不動点、沈点などと呼びます。
また、十分な時間経過後にその力学系が漸近する集合はアトラクタと言われます。
この場合、$x = 0$がアトラクタと言われます。
アトラクタ
アトラクタとは英語の引きつける意味のattractから生まれた名詞です。
ある力学系がそこに向かって時間発展をする集合のことであり、その力学系においてアトラクタに十分近い点から運動するとき、そのアトラクタに十分近いままであり続けます。
余談ですが、一般的に、力学系は分析対象となる系の構造が明らかでない場合や、すべての状態変数を観測することが困難な場合が多いです。
そのため、1個の状態変数からd個の状態変数を復元するターケンスの埋め込み定理というのを用いることで、アトラクタを再構成することができます。
$1 < a \leqq 2$のとき
$a$が$1 < a < \leqq2$のとき、ロジスティック写像は不動点である$1-\frac{1}{a}$へ収束します。
ここでの初期値は$x_0=0.1$です。
$2 < a \leqq 3$のとき
初期値0、1を除いてロジスティック写像は不動点である$1-\frac{1}{a}$へ収束します。
このとき、単調増加または単調減少ではなく、不動点の周囲をグルグル周りながら収束していきます。
$3 < a \leqq 3.449....$のとき
ロジスティック写像は不動点に収束するのではなく、不動点の周りをグルグル周って2つの値を交互に取る動きをします。
図のように交互に2つの点を取ることを、周期点や平衡点と呼びます。このとき、周期点を2周期点といい、そしてその振る舞いを2周期軌道などと呼びます。
不動点と同様に、周期点にも安定なものと不安定なものが存在します。$3 < a \leqq 3.449....$の範囲における2周期点は安定周期点です。
下図は、$x_t$と$t$の関係性を表した図です。値がずっと2つの値を取り続けていくのがわかります。
$3.449... < a \leqq 3.569....$のとき
$a$が$3.449... < a \leqq 3.569....$のとき、ロジスティック写像は安定な4周期軌道の状態になります。
つまり、グルグルと回りながら4つの値を取り続けます。
このパタメータ$a$の値を大きくしていくと、ロジスティック写像では4周期から8周期、8周期から16周期、16周期から32周期軌道の状態へと動きが変わっていきます。例えば、$a=3.56$ならば8周期です。
この軌道の状態が$a$の値によって変わることを周期倍分岐と言います。
※実行速度、エポック数は今までと異なる設定になっております。
$x_t$と$t$の関係性を表した図を見ると、値がずっと4つの値を取り続けていることが確認できます。
$3.569... < a \leqq 4....$のとき
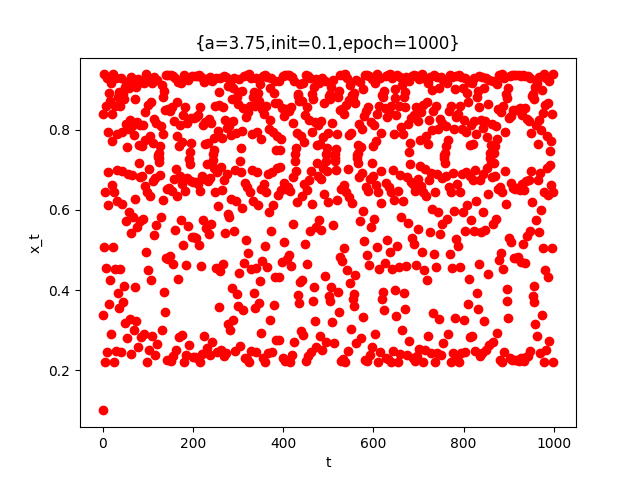
$a$が3.449を超えると、ロジスティック写像ではカオスが発生します。
カオス
カオスとは、収束も周期性も無く不規則で複雑な挙動のことです。
厳密に何を持ってカオスを定義するかを話すのは難しいです。ここでは、まったく予測が困難なデタラメな動きのことをカオスだと思って下さい。
$x_t$と$t$の関係性を表した図を見てみます。
値がデタラメ取り続けられていることがわかります。
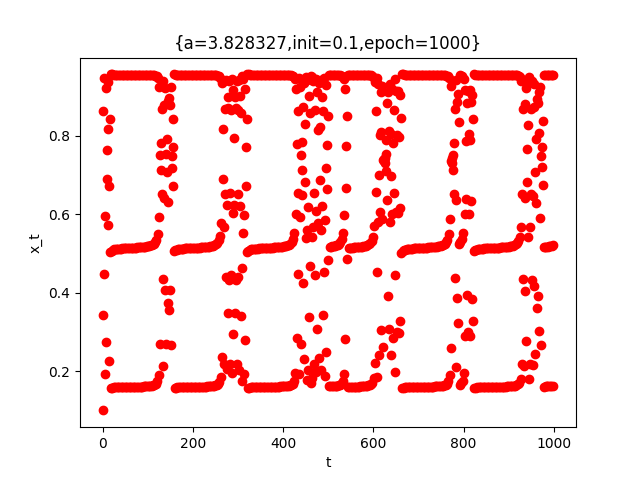
しかし、$3.569... < a \leqq 4....$では、常にカオス軌道を示す訳ではありません。$a$の値の領域によってはカオス軌道になったり周期軌道になったりする場合もあります。
例えば、$a=3.828327$のときだと下のようにカオス軌道になったり周期軌道になったりしています。
$ 4 \leqq a $のとき
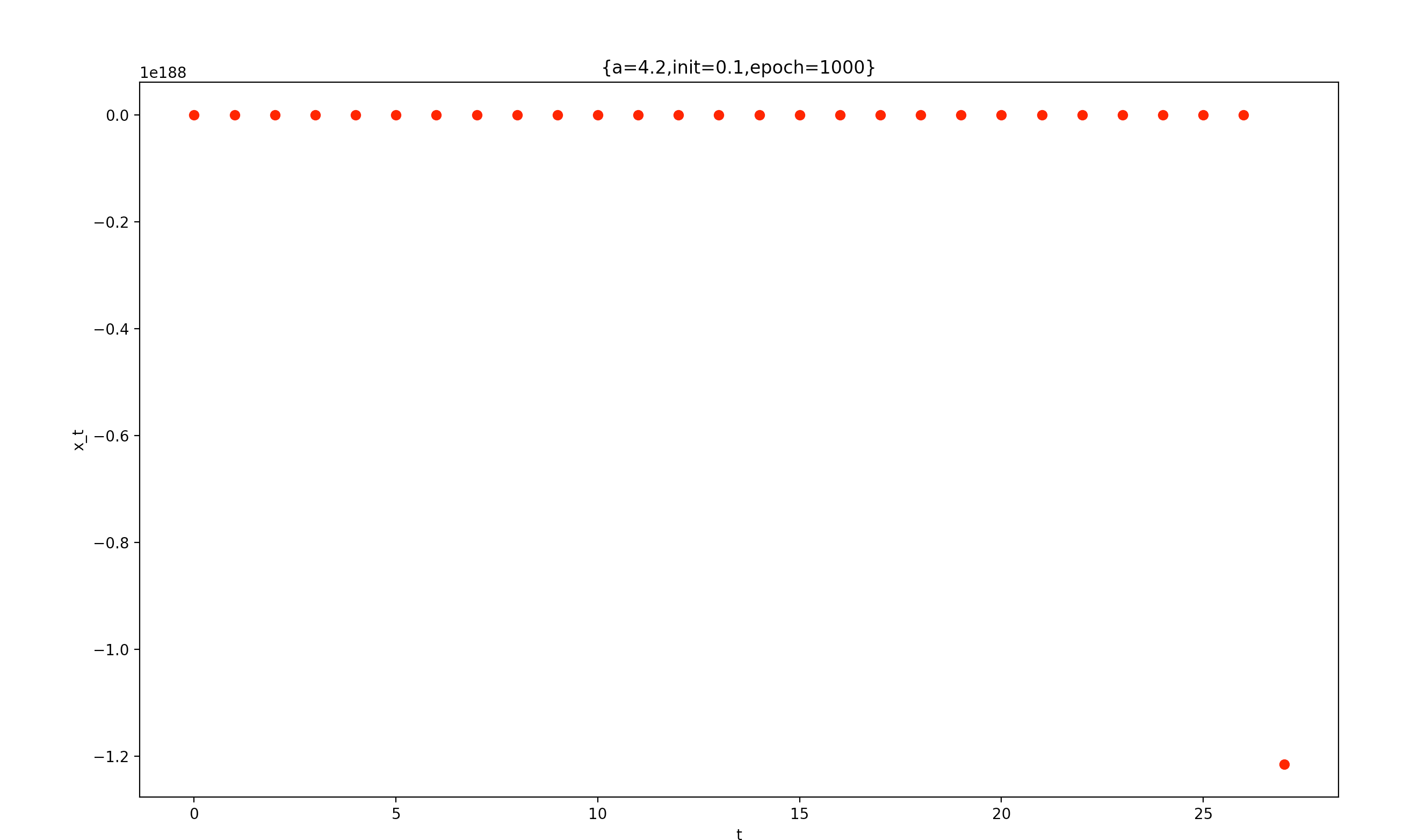
a が 4 を超えるとほとんどの初期値$x_0$から始まる挙動はマイナス無限大へ発散してしまいます。
そのため、描画はできませんが描画してみます。
軸の値を見るとわかりますが、マイナス無限大方向へ発散してしまっています。
$x_t$と$t$の関係性を表した図を見てみます。
軸の値を見るとわかりますが、マイナス無限大方向へ発散してしまっています。
まとめ
ここまでロジスティック写像のパラメータ$a$の値による振る舞いを見てきました。
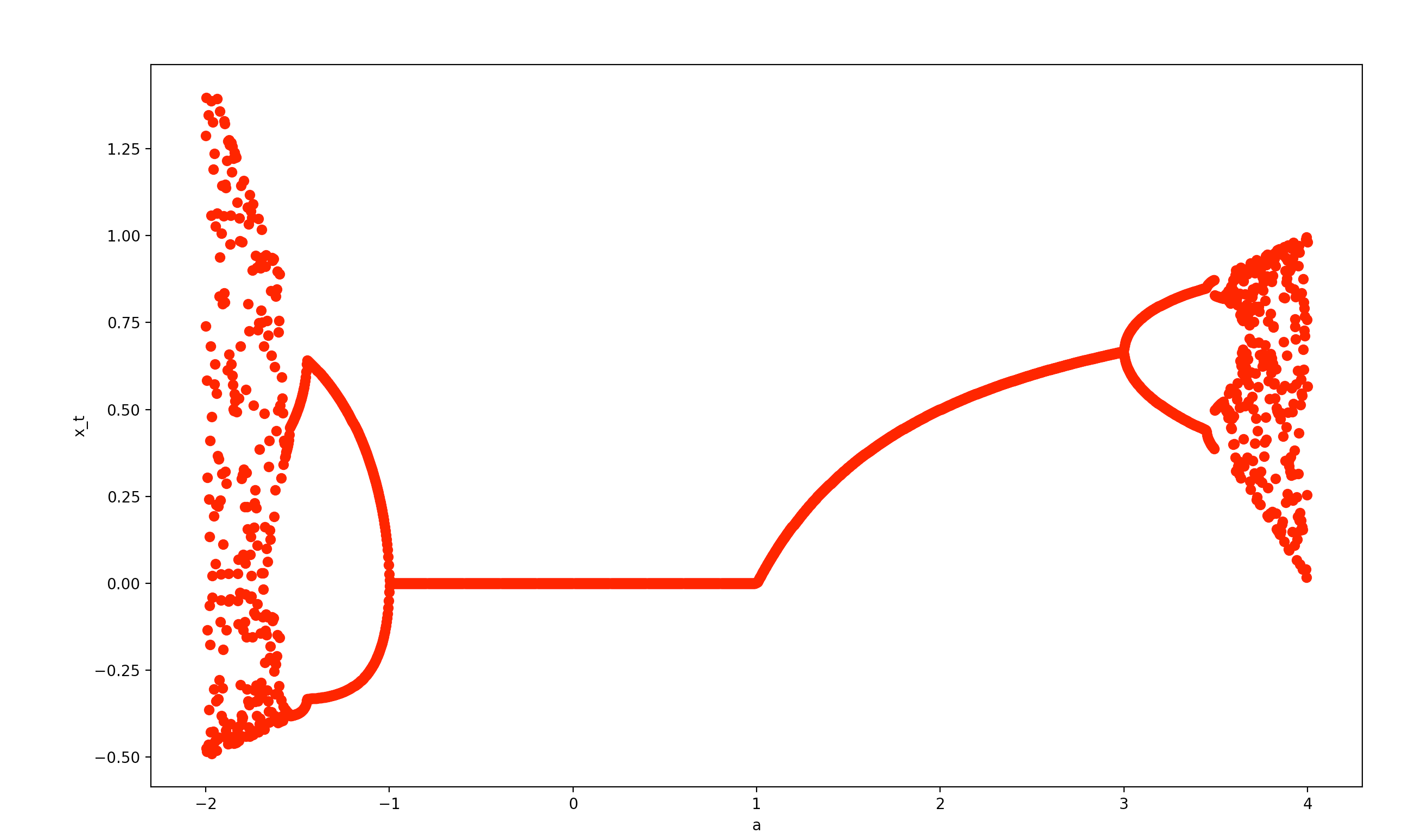
最後に横軸を$a$、縦軸を$x_t$として図にプロットしてみます。
最初1つの値に収束し、それが2つの値に収束する2周期軌道へなり、2周期から4周期、4周期から8周期、8周期から16周期、16周期から32周期... と周期倍分岐が発生しています。そしてカオスが発生して発散に至るのです。また、$a$が負の範囲のときの写像の分岐は、正の場合と似たような分岐になっていることがわかります。
おまけ
ここからは余談になります。
個人的に気になったことを挙げていきます。
非線形関数の証明
ロジスティック写像は非線形性関数です。この証明をしていきます。
線形写像の定義は次のようになります。
線形写像の定義
を$\mathbb{F}$上のベクトル空間とするとき、$f: V \rightarrow W$が線形写像であるには
$$f(\boldsymbol{x}+\boldsymbol{y}) = f(\boldsymbol{x}) + f(\boldsymbol{y}), \quad \boldsymbol{x}, \boldsymbol{y} \in V$$
$$f(\boldsymbol{x}) = kf(\boldsymbol{x}), \quad k \in \mathbb{F}$$
の両方が成立する必要がある。
この条件を満たすには以下の式が成り立たなくてはいけません。
$$f(x + y) -f(x) - f(y) = 0$$
ロジスティック写像は$f(x)=ax(1-x)$なので
$$a(x+y)(1-x-y) - ax(1-x) - ay(1-y) = 0$$
変形して計算していくと
$$x+y-x^2-xy-xy-y^2-x+x^2-y+y^2=0$$
$$-2xy = 0$$
従って、ロジスティック写像は線形写像の条件を満たさないので非線形関数である。
線形写像
線形写像の条件を満たすもには基本的に1次関数です。そのため、2次関数であるロジスティック写像は満たさないです。
終わりに
ロジスティック写像の実装ですが、思った以上に組むことが難しかったです。$a$の値をコンマ単位で変えるだけで挙動が大きく変わるため非常に繊細なものだと思いました。
ここまで読んでくださりありがとうございます。
修正リクエストをお待ちしてます。