最近、GPDMの論文を読んでるのですがGPLVMの理解が必須と思いまして、pythonで実装をしてみました。
本記事では、そのGPLVMについての記事になります。
概要
ガウス過程潜在変数モデル(GPLVM)は、ガウス過程を使って(潜在的に)高次元データの低次元表現を教師なし学習する次元削減方法です。
GPLVMは拡張性が高く理論的に扱いやすいという魅力があります。
本記事では、ガウス過程の青本を参考にしました。
問題設定
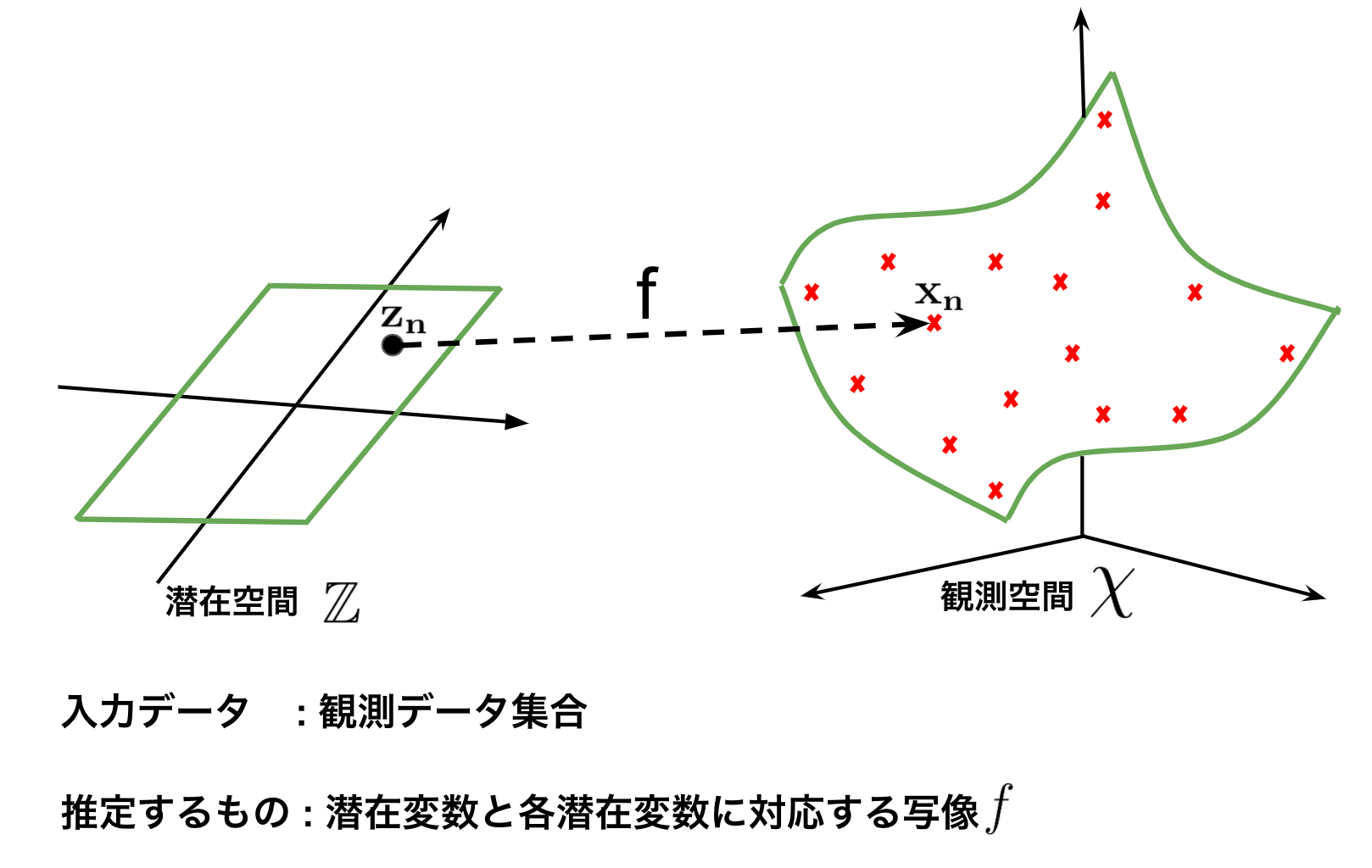
$N$個の観測データを$\mathbf X = \{\mathbf x_n \}^N_{n=1}, \mathbf x_n \in \mathcal X$が与えられたとき、$\mathcal{X}$ は高次元の観測空間で、$D$次元のユークリッド空間とします。つまり$\mathcal X = \mathbb R^D$であり、データ全体は$\mathbf X \in \mathbb R^{N \times D}$と表せます。
$\mathbf{X}$は各次元で別々の意味を持ち、近い$\mathbf{z}$同士では近い値になっていると考えます。ここで、$N$個の$\mathbf{x_n}$のそれぞれに対応した未知の$N$個の潜在変数$\mathbf{Z}=\{\mathbf{z_n}\}^N_{n=1}$からのガウス過程回帰での写像$f$によって生成されると仮定します。GPLVMは、この写像$f$を推定します。
実装
GPLVMでは観測データ同士が近いところにあれば、それらに対応する潜在変数も近いところにあると考えます。
$N$個の$\mathbf{x_n}$のそれぞれに対応した未知の$N$個の潜在変数$\{\mathbf{z_n}\}^N_{n=1}$からのガウス過程回帰での写像$f$によって生成されると仮定しているので、$\mathbf{Z}$がわかれば、それぞれの各出力次元は独立なので、データ$X$全体の確率は、各データの次元の和になります。
$$p(\mathbf{X}|\mathbf{Z})=\prod_{d=1}^D p(\mathbf{x}|\mathbf{Z})=\prod_{d=1}^D N(\mathbf{x}|0, \mathbf{K_z}+\sigma^2 \mathbf{I})$$
ここで$\mathbf{x}$は平均が$0$で、ガウス分布による誤差を考えて以下の式で表せられるとしています。また、それぞれの$\mathbf{z}$が$K$次元の標準ガウス分布に従うと考えます。
$$\mathbf{x} \sim (0,\mathbf{K_z}+\sigma^2\mathbf{I})$$
$$p(\mathbf{X})=\prod_{n=1}^N p(\mathbf{z_n}),\,\,\,\,p(\mathbf{x})=N(0,\mathbf{I_K})$$
これらのことから$\mathbf{X}$と$\mathbf{Z}$の同時確率は次のように表すことができます。
$$p(\mathbf{X},\mathbf{Z})=p(\mathbf{X}|\mathbf{Z})p(\mathbf{Z})=\prod_{d=1}^DN(\mathbf{x}|0,\mathbf{K_z}+\sigma^2\mathbf{I})\prod_{n=1}^NN(\mathbf{z_n}|0,\mathbf{I_K})$$
GPLVMでは、この式(が最大となるような$\mathbf{Z}$を見つけます。
詳細な計算は省きますが、この式を変形して対数尤度を考えると下記の式になります。このとき、青本では$\prod_{n=1}^NN(\mathbf{z_n}|0,\mathbf{I_K})$の対数尤度(おそらく正則化項)は無視しています・
$$L=\log p(\mathbf{X}|\mathbf{Z})=-\frac{ND}{2}\log(2\pi)-\frac{D}{2}\log|\mathbf{K_z}|-\frac{1}{2}tr(\mathbf{K_z^{-1}}\mathbf{Y}\mathbf{Y}^T)$$
観測変数の対数尤度$L$から潜在変数の更新の勾配法を求められます。計算していくと下記の式が導けます。
$$\frac{\partial L}{\partial \mathbf{K_z}}=\frac{1}{2}(\mathbf{K^{-1}_x}\mathbf{Y}\mathbf{Y}^T\mathbf{K_z^{-1}}-D\mathbf{K_z^{-1}})$$
$$\frac{\partial \mathbf{K_z}}{\partial \mathbf{x}}=-2k(\mathbf{z_n},\mathbf{z}_n^{\prime})(z_{nj}-z_{n^{\prime}j})/\sigma$$
このとき、カーネル関数は下記のガウスカーネルを用いています。$\delta$のところは$n=n^{\prime}$ならば$1$となり、それ以外は$0$になります。
$$K(z,z^{\prime})=\theta_1\exp\left(-\frac{|z_n-z_n^{\prime}|^2}{\theta_2}\right)+\theta_3\delta(n,n^{\prime})$$
潜在変数の更新と写像の推定
したがって$\frac{\partial L}{\partial \mathbf z}=\frac{\partial L}{\partial \mathbf{K_z}}\frac{\partial \mathbf{K_z}}{\partial \mathbf{x}}$より、潜在変数の更新と写像の推定は以下の式で行います。
潜在変数の更新(勾配法)
$\frac{\partial L}{\partial \mathbf z}$はマイナスなので下記の式になります。
$$\mathbf{z}=\mathbf{z}+\frac{\partial L}{\partial \mathbf z}$$
写像の推定
GPRを用いています。青本では太字を横ベクトルで表していますが、実装するときは縦ベクトルで考えているので転置のところは消えています。
$$f(\mathbf{z}) \sim \mathcal{GP}(\mathbf{K}(\mathbf{z},\mathbf{z}^{\prime})(\mathbf{K}(\mathbf{z},\mathbf{z}))^{-1}\mathbf{X},\,\,\,\,\mathbf{K}(\mathbf{z}^{\prime},\mathbf{z}^{\prime})-\mathbf{K}(\mathbf{z},\mathbf{z}^{\prime})(\mathbf{K}(\mathbf{z},\mathbf{z}))^{-1}\mathbf{K}(\mathbf{z},\mathbf{z}^{\prime}))$$
実装コードと結果
import numpy as np
import matplotlib.animation as animation
import matplotlib.pyplot as plt
from scipy.spatial import distance as dist
from tqdm import tqdm
class GPLVM(object):
def __init__(self, θ1, θ2, θ3):
self.θ1 = θ1
self.θ2 = θ2
self.θ3 = θ3
def fit(self, X, latent_dim, epoch, eta):
resolution = 10
T = epoch
N, D = X.shape
L = latent_dim
Z = np.random.randn(N, L) /100
history = {}
history['Z'] = np.zeros((T, N, L))
history['f'] = np.zeros((T, resolution, resolution, D))
for t in tqdm(range(T)):
K = self.θ1 * self.kernel(Z, Z, self.θ2) + self.θ3 * np.eye(N)
inv_K = np.linalg.inv(K)
dLdK = 0.5 * (inv_K @ (X @ X.T) @ inv_K - D * inv_K)
dKdX = -2.0*(((Z[:,None,:]-Z[None,:,:])*K[:,:,None]))/self.θ2
dLdX = np.sum(dLdK[:, :, None] * dKdX, axis=1)
Z = Z + eta * dLdX
history['Z'][t] = Z
z_new_x = np.linspace(min(Z[:,0]),max(Z[:,0]), resolution)
z_new_y = np.linspace(min(Z[:,1]),max(Z[:,1]), resolution)
z_new = np.dstack(np.meshgrid(z_new_x, z_new_y)).reshape(resolution**2, L)
k_star = self.θ1 * self.kernel(z_new, Z, self.θ2)
F = (k_star @ inv_K @ X).reshape(resolution, resolution, D)
history['f'][t] = F
return history
def kernel(self,X1, X2, θ2):
Dist = np.sum(((X1[: , None, :] - X2[None, :, :])**2), axis=2)
K = np.exp((-0.5/θ2) * Dist)
return K
if __name__ == "__main__":
np.random.seed(0)
resolution = 100
z1 = np.random.rand(resolution) * 2.0 - 1.0
z2 = np.random.rand(resolution) * 2.0 - 1.0
X = np.empty((resolution, 3))
X[:, 0] = z1
X[:, 1] = z2
X[:, 2] = (z1**2 - z2**2)
X += np.random.normal(loc=0, scale=0.0, size=X.shape)
model = GPLVM(θ1=1.0, θ2=0.03, θ3=0.05)
history = model.fit(X,latent_dim=2, epoch=100, eta=0.00001)
# ---------描写---------------------------------------------------------------
fig = plt.figure(figsize=(10, 5))
ax_observable = fig.add_subplot(122, projection='3d')
ax_latent = fig.add_subplot(121)
def update(i, z, x, f):
plt.cla()
ax_latent.cla()
ax_observable.cla()
fig.suptitle(f"epoch: {i}")
ax_latent.scatter(z[i,:, 0], z[i,:, 1],s=50, edgecolors="k", c=x[:,0])
ax_observable.scatter(x[:, 0], x[:, 1], x[:, 2], c=x[:,0],s=50, marker='x')
ax_observable.plot_wireframe(f[i ,:, :, 0], f[i, :, :, 1], f[i, :, :, 2], color='black')
ax_observable.set_xlim(x[:, 0].min(), x[:, 0].max())
ax_observable.set_ylim(x[:, 1].min(), x[:, 1].max())
ax_observable.set_zlim(x[:, 2].min(), x[:, 2].max())
ax_observable.set_title('observable_space')
ax_observable.set_xlabel("X_dim")
ax_observable.set_ylabel("Y_dim")
ax_observable.set_zlabel("Z_dim")
ax_latent.set_title('latent_space')
ax_latent.set_xlabel("X_dim")
ax_latent.set_ylabel("Y_dim")
ani = animation.FuncAnimation(fig, update, fargs=(history['Z'], X, history['f']), interval=100, frames=100)
# ani.save("tmp.gif", writer = "pillow")
print("X: {}, Y: {}, Z:{}".format(X.shape, history['f'][0].shape, history['Z'][0].shape))
plt.show()
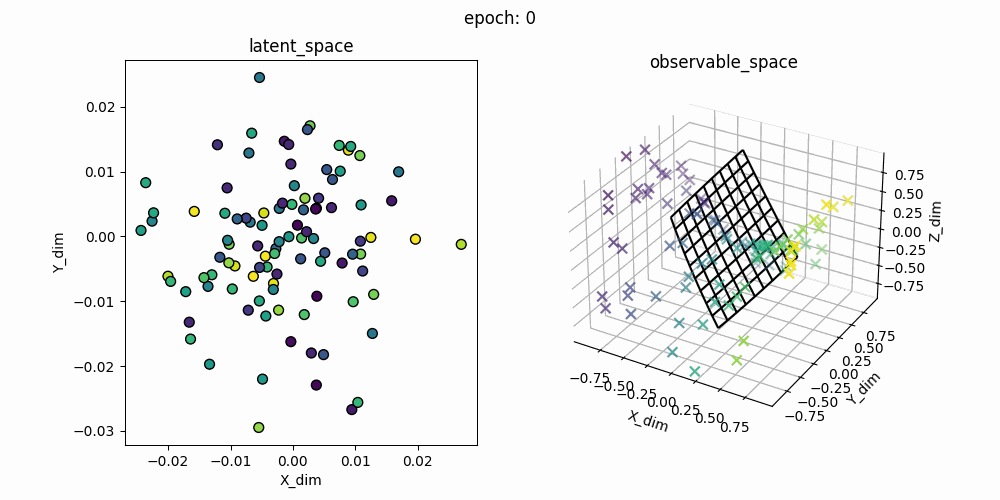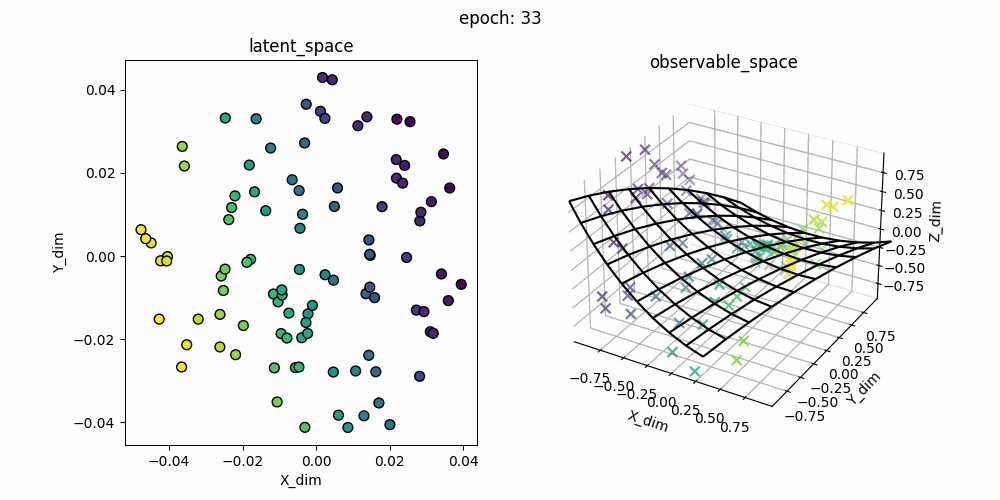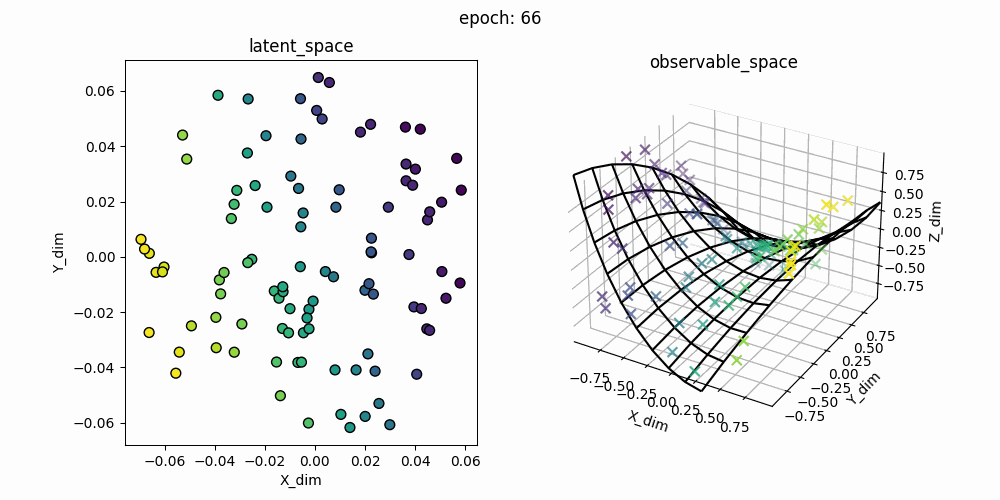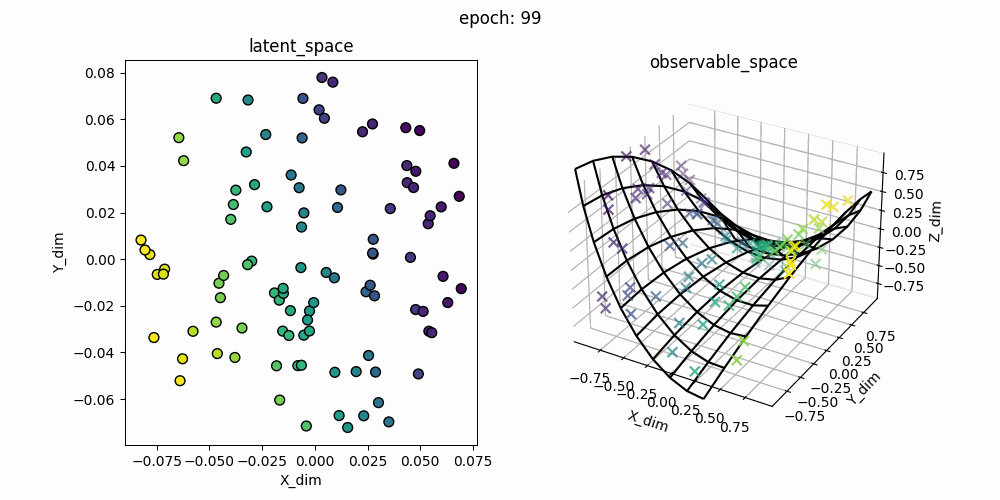
右図が観測空間上での推定した多様体の学習過程で、右図はその時の潜在変数です。ハイパーパラメータを手動で探しましたが、綺麗に描画してくれるのを見つけるのに苦労しました。コンマ単位でハイパーパラメータを変えると描画ができなくなってしまいます。GPLVMがそれだけ繊細なモノということを実感しました。
参考文献
ガウス過程と機械学習 (機械学習プロフェッショナルシリーズ)
終わりに
ここまで読んでくださってありがとうございます。
編集リクエストもお待ちしてます。