本記事では主成分分析の実装をしたいと思います。主成分分析の理論については下記の記事を参考にして下さい。
-

-
PCAについて理解したい(理論編)
この記事は古川研究室 Advent Calendar13日目の記事です。 本記事は古川研究室の学生が ...
続きを見る
主成分分析のアルゴリズムは理論編にて話しました。本実装では、そのアルゴリズムを実装したいと思います。
PCAのアルゴリズム
①$x_i-\overline{x}$により中心化を行う
②分散・共分散行列$X^TX$を解く
③下記の固有値問題を解く$$\max_{\lambda}~\Omega w = \lambda w~~~~~~~~~subject~~to~~~~~~~\lambda\geqq0$$
④得られる固有値$\lambda$をそれぞれ$\lambda_1 \geqq \lambda_2 \geqq \lambda_2 \dots \geqq \lambda_d \geqq 0$とする。
⑤それぞれの固有値に対応する固有ベクトル$w_1,w_2,\dots,w_d$を主成分軸の正規直交基底とし、縮小したい次元(2次元なら2個)分を選択する。このとき、$w_1,w_2,\dots$を順に第1主成分、第2主成分,,,となる。
⑥選択した固有ベクトル$w_1,w_2\dots,w_D$の行列$W(w_1,w_2\dots)$の行列を作成し、学習データを低次元空間へ写像したときの主成分得点$F=(f_1(x_1),f_2(x_2),\dots,f_D(x_D))$を算出する。
$$F(X)=XW$$
使用データ
irisのデータを使用します。irisデータとは、アヤメという花の3つの種類であるstosa、versicolor、virginicaの萼の長さ(sepal length)、 萼の幅(sepal width)、花弁の長さ(petal length)、花弁の幅(petal width)のことを言います。

これら全てのデータが下記のコードの変数Xにあります。上の図は変数Xをprint文で出力した結果です。
# データの準備
from sklearn.datasets import load_iris
import pandas as pd
dataset = load_iris()
iris = load_iris()
X = pd.DataFrame(iris.data,
columns=iris.feature_names)
#X.shape : (150,4)
中心化
irisデータ(変数X)に対して中心化の処理を行います。
# データの準備
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
dataset = load_iris()
iris = load_iris()
X = pd.DataFrame(iris.data,
columns=iris.feature_names)
#X.shape : (150,4)
# ---------------------------------
# 追加コード
mean = np.mean(X, axis=0)
X = X - mean
axis=0というのは列ごとに平均を取るという意味です。つまり、花の4つの特徴(次元)でそれぞれの平均を算出して、中心化を行っています。
分散・共分散行列$X^TX$を解く
コードは次のようになります。lowerdim変数に何次元に落とし込みたいのかの数値を代入します。
# データの準備
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
dataset = load_iris()
iris = load_iris()
X = pd.DataFrame(iris.data,
columns=iris.feature_names)
#X.shape : (150,4)
mean = np.mean(X, axis=0)
X = X - mean
# ---------------------------------
# 追加コード
lowerdim = 2 #任意の次元へ低次元化
cov = np.cov(X.T, bias=1) #分散共分散行列
L, V = np.linalg.eig(cov) # 固有値問題
inds = np.argsort(L)[::-1] # 固有値の降順ソート
L = L[inds]
W = V[:, inds]
F = np.matmul(X, W[:,:lowerdim]) #主成分得点
1つずつ見ていきたいと思います。
cov = np.cov(X.T, bias=1) #分散共分散行列
L, V = np.linalg.eig(cov) # 固有値問題np.covを使うことでデータXの分散共分散行列を計算しています。ここで、bias=1はbias=Trueと同じ意味です。これは、標本分散(データ数でわる)ということになっています。
そして、この得られた分散共分散行列に対しての固有値問題をnp.linalg.eig()を使うことで、固有値と固有ベクトルをタプルで受け取ります。
inds = np.argsort(L)[::-1]
L = L[inds]
W = V[:, inds]得られた固有値をnp.argsortで小さい順から並ぶようにソートします。ここで、[::-1]というのはsort関数が昇順にソートし、argsort関数は昇順にソートしたインデックスの配列を返すために、[::-1]というスライスの書き方を使って降順にしています。
F = np.matmul(X, W[:,:lowerdim])このコードでは主成分得点を求めています。
$$F(X)=XW$$
描画してみる
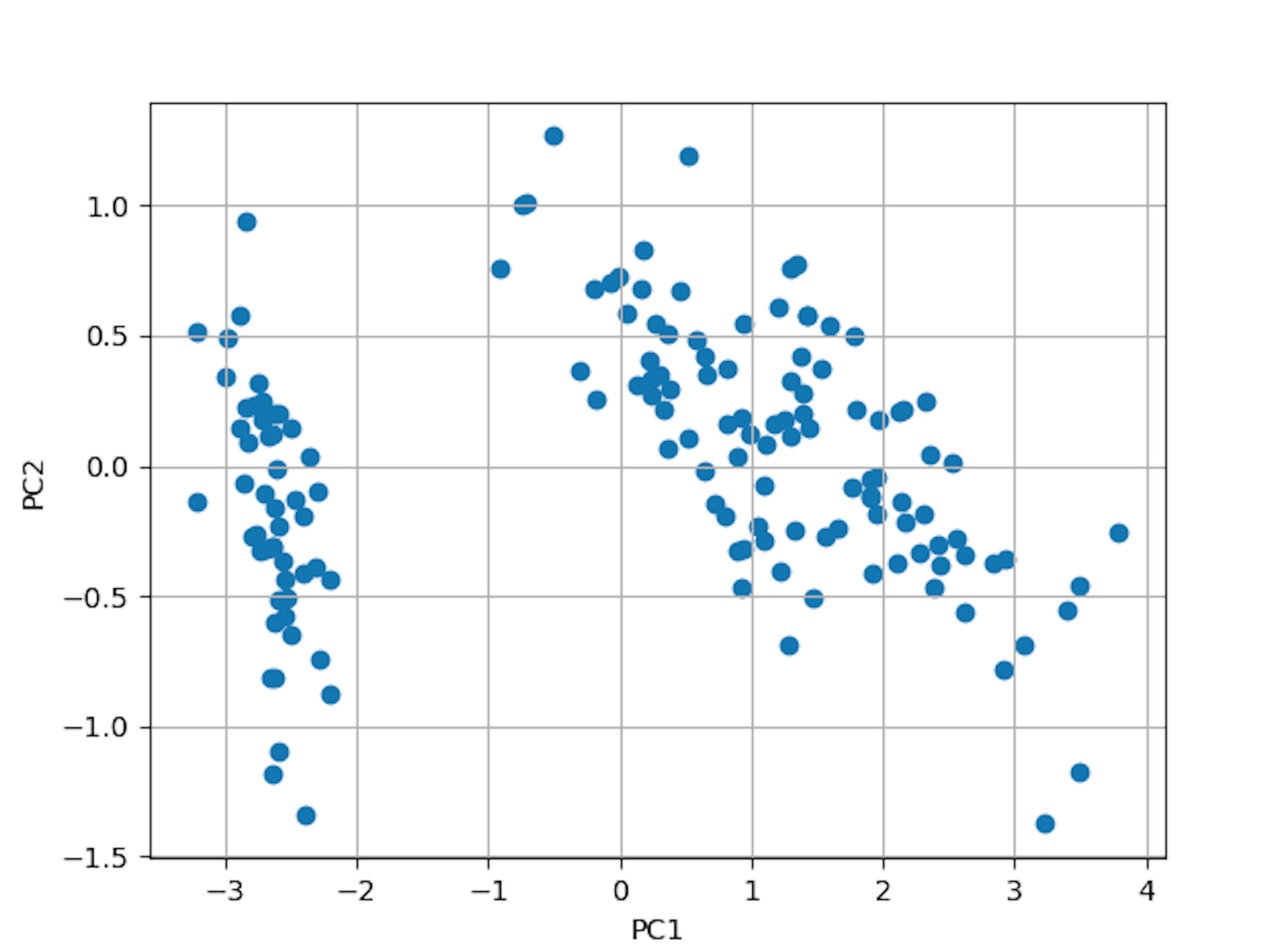
実装コードをまとめてmatplotlibで描画してみました。
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
dataset = load_iris()
iris = load_iris()
X = pd.DataFrame(iris.data,
columns=iris.feature_names)
lowerdim = 2 #任意の次元へ低次元化(この場合は2次元)
mean = np.mean(X, axis=0)
X = X - mean
cov = np.cov(X.T, bias=1)
L, V = np.linalg.eig(cov)
inds = np.argsort(L)[::-1]
L = L[inds]
W = V[:, inds]
F = np.matmul(X, W[:,:lowerdim])
fig = plt.figure()
plt.scatter(F[0], F[1])
plt.grid()
plt.xlabel("PC1")
plt.ylabel("PC2")
fig.savefig("img.png")
plt.show()4次元データであったirisデータが2次元へ削減されています。lowerdim = 2のところを3に変えると3次元への削減となります。
主成分分析での次元削減の実装ができました。
どのくらいの精度で次元削減できたのか?
次元削減できましたが、どの程度信頼していいのでしょうか?
それを図る指標として寄与率と累積寄与率というものがあります。
寄与率
主成分軸一つが、データの何割を説明することができているか」を表したものであり、各主成分の固有値の総和に対しての割合として下記の式で定義されています。
$$第k主成分軸の寄与率=\frac{\lambda_k}{\sum_{k^{\prime}=1}\lambda_k^{\prime}}\times 100$$
$\lambda_k$は第$k$主成分の固有値のことです。
累積寄与率
累積寄与率とは、第1主成分から第m主成分までの寄与率の和のことです。
これにより、第1主成分から第m主成分での削減がデータの散らばり具合をどの程度カバーしているかの説明する割合がわかります。
$$第m主成分までの累積寄与率 = \frac{\lambda_1+\lambda_2+\dots+\lambda_m}{\sum_{m^{\prime}=1}\lambda_m^{\prime}}\times 100$$
実際に実装で見てみます。
#寄与率
cont = L / np.sum(L) * 100
#累積寄与率
comCont = [np.sum(cont[:i+1]) for i in range (len(L))]この結果、下のような結果になりました。
cont(寄与率) [92.46187232 5.30664831 1.71026098 0.52121839]
comCont(累積寄与率) [92.4618723201727, 97.76852063187947, 99.47878161267244, 99.99999999999999]累積寄与率を見ると、第1主成分でデータの92%、第1主成分でデータの97%も表現できています。したがって、今回の主成分分析は信頼できるものと判定できます。
主成分軸の意味
第1主成分、第2主成分ともに高い割合で情報を持っていましたが、これはirisデータの何のデータが高い割合を占めているのかが気になります。
これは、第1主成分、第2主成分の正規直行基底を見ればわかります。それはコードの変数Wをみるとわかります。
print(W[:,[0]])
print(W[:,[1]])
#------------------------------------
[[ 0.36138659]
[-0.08452251]
[ 0.85667061]
[ 0.3582892 ]]
[[-0.65658877]
[-0.73016143]
[ 0.17337266]
[ 0.07548102]]
irisデータでは、萼の長さ(sepal length)、萼の幅(sepal width)、花弁の長さ(petal length)、花弁の幅(petal width)の順に特徴量があります。第1主成分の結果の3番目は0.856(85.6%)と大きな数値があります。
つまり、第1主成分では、花弁の幅(petal width)が最も相関があるということがわかります。
また、第2主成分では、1番目と2番目の数値が負の値で大きいことから、萼の長さ(sepal length)と萼の幅(sepal width)の情報が最も相関があるということがわかります。
主成分負荷量
固有値を用いて表現した主成分軸は、データの単位や値の範囲に影響を受けます。
そこで、そういった影響をなくすために主成分得点や元データとの相関を表すものがあります。それが主成分負荷量というものです。
主成分負荷量
主成分負荷量とは主成分得点と元データとの相関係数を表現したものである。単位や値の範囲の影響を受けないため主成分軸の解釈がしやすいものです。
$$元データ特徴量x_{q}と主成分得点f_{l}(x)との相関係数 = \frac{\sum_{x_q,f_l}}{\sqrt{\sum_{x_q}}\sqrt{\sum_{f_l}}}$$
$$f_l(x)は第l主成分の主成分得点f_l(x)=xw_l$$
これを実装して挙動の確認をしてみます。
tmp = np.concatenate([X,F],axis=1)
PCL = np.corrcoef(tmp.T, bias=1)[:X.shape[1], -F.shape[1]:]np.concatinateで列方向でデータと主成分得点を結合しています。
データと主成分得点間の相関係数を順に取り出します。
結果はこちらです。
[[ 0.89740176 -0.39060441]
[-0.39874847 -0.82522871]
[ 0.99787394 0.0483806 ]
[ 0.96654752 0.0487816 ]]
第1主成分軸(第1列)は萼の長さ、花弁の長さ、花弁の幅の値が大きく相関が強いことがわかります。つまり、第1主成分軸は花弁の長さだけでなく、萼の長さ、花弁の幅にも対応しているということです。また、第2主成分軸(第2列)は萼の幅だけが負の値で大きいことから、萼の幅に対応したものであるというのがわかります。
終わりに
因子分析についても書きたかったですが、本記事ではここまでにしておきます。
ここまで読んでくださってありがとうございました。
編集リクエストもお待ちしてます。